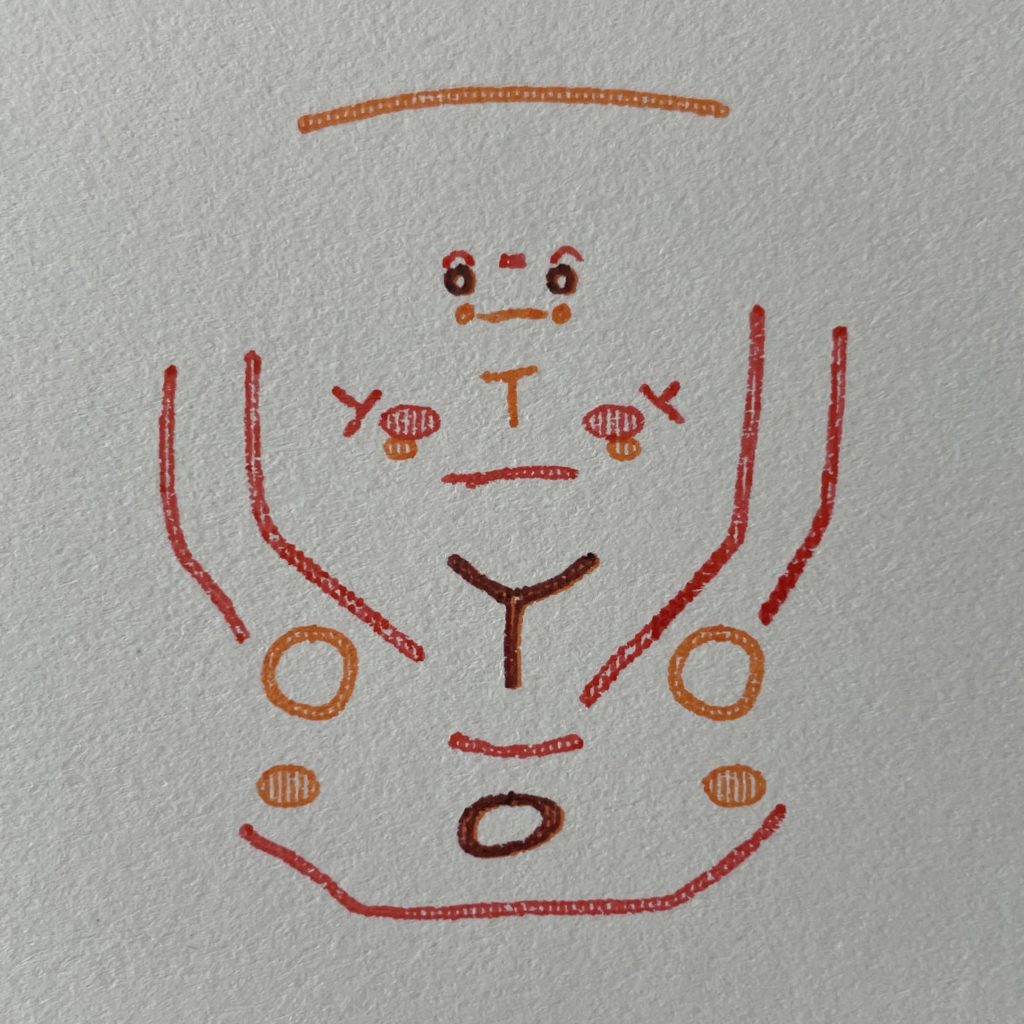
Face illustrations generated using a simple substitution grammar and then plotted to paper.
Detail:
face generator
genetic algorithm for line drawings
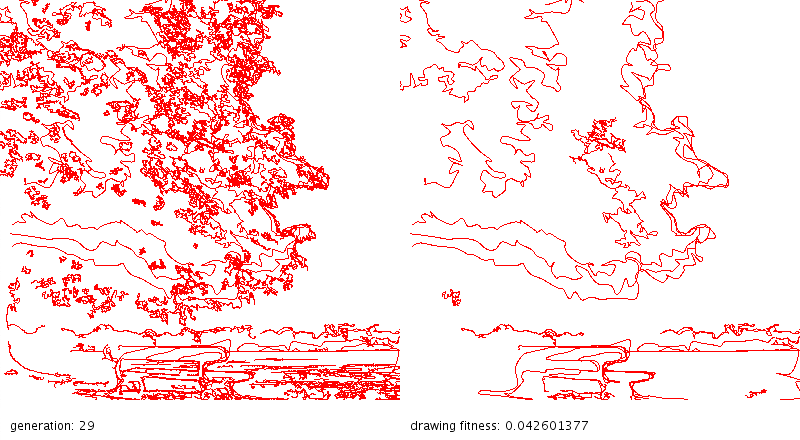
These drawings were extracted from images using a combination of OpenCV and a genetic algorithm.
First, OpenCV is used to find contour lines and canny edges in the images. On the left are all the lines found this way (typically hundreds of lines) that have been post-processed a bit to smooth longer lines.
On the right are 20 lines selected by the genetic algorithm. The algorithm generates 100 drawings, each with a different set of lines from the drawing on the left. It then automatically evaluates the fitness of each drawing and creates a new generation of 100 drawing, selecting characteristics more often from the highest rated drawings and tossing in some random mutations.
The goal is to capture the essence of the original image in just a few vector lines so that a drawing robot can efficiently recreate it. Below are more examples.
More Genetic Algorithm Drawings
Some more sample results from a drawing app I am working on that uses a genetic algorithm to generate drawing (click for higher resolution):
Above: face 1, Below: face 2 (same source image as face 1)
Above: one generation of faces (same source as face 1 and 2)
Above: face 3 (different source image), Below: landscape.
Portrait Drawing with Genetic Algorithm
Some results from a drawing program I am working on that uses a genetic algorithm to refine the drawing style. Below is the first generation.
First Generation (above) and 4th (below)
4th (above) and 7th generation (below)
The 7th generation (above) and the 16th image in that generation below. 
Mutants
The effects of mutations in one generation of spirographs. Choosing only one graph to survive from the previous generation (not a natural thing to do) results in 36 offspring from the one graph. It is an good way to check the impacts of mutations in the genetic algorithm and has an interesting outcome. The parent graph is below.
Eggbot eggs 2015 : genetic algorithm
This year’s addition to my eggbot programs is a genetic algorithm that evolves complex sine waves. Each of the eggs in the photo above was printed from the same program with waves evolved from random seeds.
The individual designs
Each design is a sine wave with eight different parameters:
- Amplitude
- Length
- The number of waves to be strung together
- Amplitude of the first modulation applied to the amplitude
- Length of the first modulation applied to the amplitude
- Amplitude of the second modulation applied to the amplitude
- Length of the second modulation applied to the amplitude
- The modulations to be used (either 1 or both 1 & 2)
The video above shows how the 8 parameters modulate the wave and how patterns build up over time.
How the genetic algorithm works
Each time the program is run, an initial population is created with 50 individual designs — each with random values assigned to the eight parameters. You then rate each individual design before evolving the next generation. The algorithm chooses individuals to carry on to the next generations (highly rated designs are more likely to be carried forward, but low rated designs may still be used).
Designs that are carried forward are likely to be bred with other designs chosen for the next generation. Breeding involves picking a random integer N between 1 and 8 and taking the first N parameters of one individual and swapping them with the first N parameters of the other. This cross-over of the parameters creates new variations of the designs with qualities of both individuals (the parents). There is also a slim chance that one or more of the child’s parameters will change (mutate) between generations.
The evolution process makes it relatively easy to search through a very wide range of possible combinations of parameter values by simply choosing designs with aspects that you like and seeing what different combinations of these qualities look like.
I found that populations of 50 individuals are broad enough to get very interesting results in fewer than 10 generations while not having to rate too many design with each evolution.
The output
Below is a collection of 10 different designs generated in the same session.
Each column in the image above shows the lineage of the design in the top row. This top row is the 5th generation. The next row down is the highest rated parent from the 4th generation. Coincidentally, neither of these designs were changed between the 3rd and 4th generation.
The code
The program is written in processing and the source is available on github.
The algorithm is not limited to sine waves. To implement your own design, modify the Indivdual.pde file with any number of parameters. All my parameters are floats between 0 and 1, but this is not a requirement so long as you adjust your this class’ mutate function to fit your variable types.
The other classes in the repository set up the UI and manage the evolution or individuals over multiple generations. You may choose to manipulate the following three variables in GA_eggbot.pde to work with different population sizes and different probabilities for crossovers and mutations.
If you do make a design of your own, let me know in the comments below.